任意の確率分布とヒストグラムの比較
SAS を用いてデータに対するヒストグラムと特定の確率分布を指定して比較を行いたい場合、UNIVERIATE procedure の histogram statement が利用できます。
ただし、UNIVERIATE procedure を用いる場合、ベータ分布、指数分布、ガンマ分布、対数正規分布、正規分布、Johnson SB 分布、Johnson
SU 分布、ワイブル分布しか指定できません。また、縦軸のスケールがパーセントとなっており、密度 (面積が 1 と等しくなるように基準化したグラフ)
に対するヒストグラムを作成してくれません。
そこで、SAS を用いて任意の確率分布を当てはめた結果と、密度に対するヒストグラムを重ね合わせて表示し、比較を行う方法について説明します。
サンプルデータ
本稿では以下のデータを用いる事にします。自由度 3 の t 分布に従う 10000 個の乱数からなるデータセットです。
data test;
do i = 1 to 10000;
call streaminit(20111222);
t = rand("t", 3);
output;
end;
任意の確率分布とヒストグラムの比較
確率分布の当てはめ
こちらについては、様々な方法が考えられますが、本稿では単純に最尤推定を行う場合を考えます。ここでは、NLMIXED procedure を用いて、任意の確率分布を当てはめる方法を紹介します。
最尤法では対数尤度関数さえ分かれば良いので、自前で対数尤度関数を書き下します (理由は不明ですが logpdf 関数を用いるとエラーが起こる場合が多いため、組み込み関数が利用できる場合は pdf
関数を用いる方が良いでしょう)。parms statement では推定したいパラメータの初期値を指定します。model statement では任意の関数に対する "最大化" を行うための
general(function) という構文を用います、左側の t の部分はデータセットに入っている変数であれば何でもかまいません。パラメータ推定値を後で利用するので、ODS output
statement を指定して推定結果を出力します。
今回は t 分布を当てはめることにします。t 分布の対数尤度関数を最大化するために、以下の様なスクリプトを作成しました。
proc nlmixed data = test;
parms df = 1;
logL =
lgamma((df+1)/2) - log(df * constant("PI"))/2 -
lgamma(df/2) - ((df+1)/2) * log(1 + t**2/df);
model t ~ general(logL);
ods output ParameterEstimates = ESTDF;
run;
上のスクリプトを実行すると以下の様な結果が得られました。t 分布を当てはめた結果、自由度の推定値は 2.9666 となりました。最尤推定量ですので妥当な結果でしょう。
Parameter Estimates
Standard
Parameter Estimate Error Lower Upper Gradient
df 2.9666 0.07551 2.8186 3.1146 -0.00008
自前ヒストグラムの作成
ヒストグラムを作るためには、データの範囲を適当な区間に分割し、各区間に入る度数 (count)、相対度数 (proportion)、相対度数の百分率 (percent)、密度 (density) などを求めて棒グラフにすればよいです。そのため、以下の様なマクロを作成しました。マクロの引数は、入力データセット名 [data]、変数名 [var]、出力データセット名 [out]、区間数 [nbreak] です。nbreak に scott、または sturges を指定した場合は、それぞれの方法を用いて自動的に区間数を決定します、数値を直接入れた場合は区間をその個数に分割します、デフォルトは scott です。また、出力データセットには、横軸の値を表わす midpoint、縦軸の count / proportion / percent / density の四種類が計算されています。この出力データセットにパラメータ推定値から計算される任意の確率分布の密度を追加すると、ヒストグラムと任意の確率分布の比較を行う事ができます。
%macro myhist(data, var, out, nbreak = scott);
data _null_;
set &data.;
call symput("n", _n_);
%if "&nbreak." = "scott" %then %do;
proc summary data = &data.;
var &var.;
output out = &out. std = std min = min max = max;
data _null_;
set &out.;
h = 3.5 * std * &n.**(-1/3);
if h > 0 then
call symput("nbreak", ceil((max - min) / h));
else
call symput("nbreak", 1);
%end;
%if "&nbreak." = "sturges" %then %do;
data _null_;
call symput("nbreak", compress(ceil(log2(&n.) + 1)));
%end;
proc summary data = &data.;
var &var.;
output out = parm min = min max = max;
data _null_;
set parm;
if max < 0 then max = -ceil(-max);
else max = ceil(max);
if min < 0 then min = -int(-min);
else min = int(min);
call symput("by", compress((max - min) / &nbreak.));
call symput("min", compress(min));
call symput("max", compress(max));
data &out.;
set &data.;
do i = 1 to &nbreak.;
if (&var. >= &min. + (i-1) * &by.) & (&var. < &min. + i * &by.) then do;
midpoint = &min. + (i-1/2) * &by.;
end;
end;
proc freq data = &out. noprint;
tables midpoint / out = &out.;
data &out.;
set &out.;
proportion = count / &n.;
density = proportion / &by.;
percent = proportion * 100;
run;
%mend myhist;
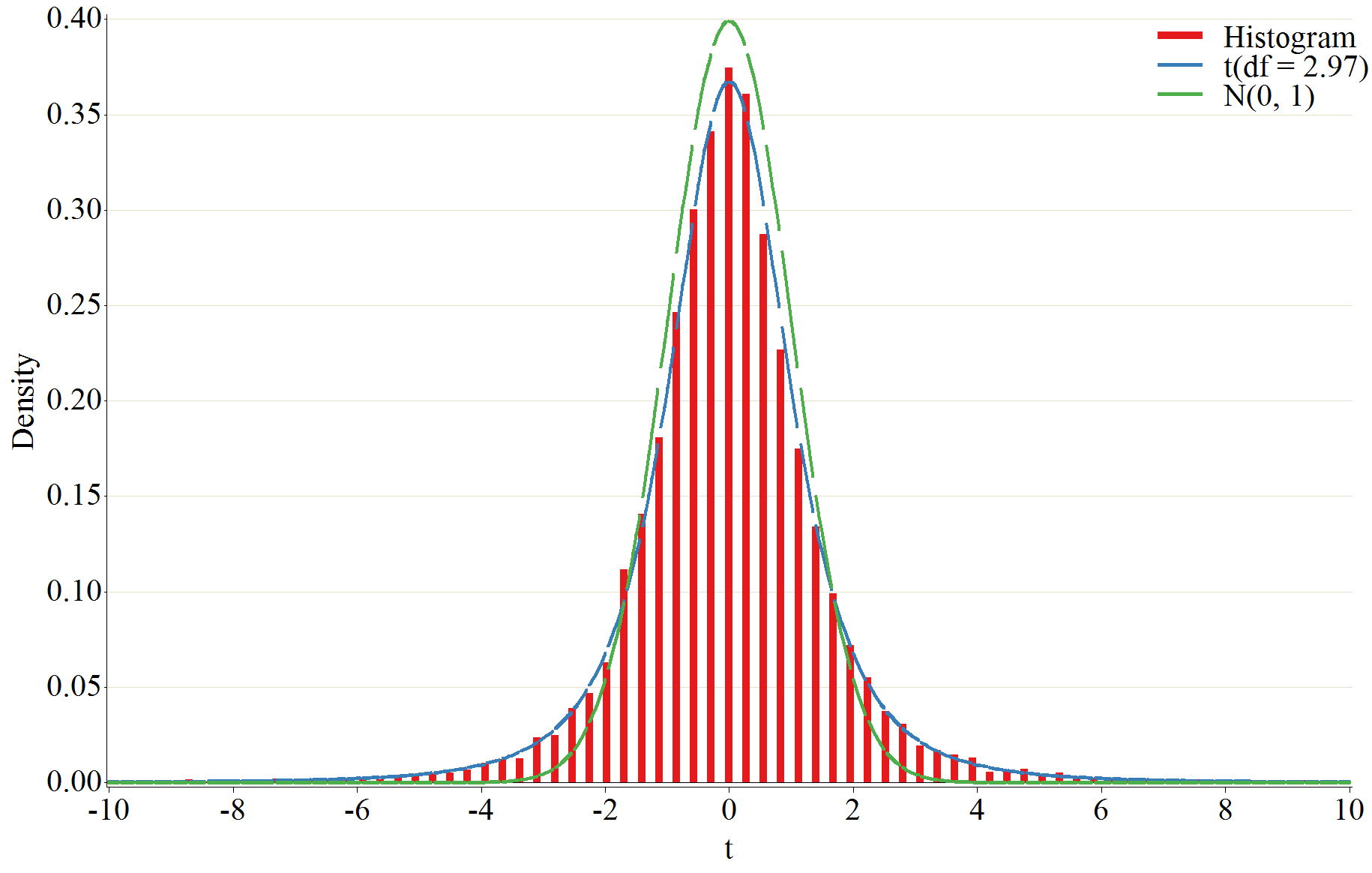
このマクロを使って、データからヒストグラムを書くための棒グラフのデータを作成し、GPLOT procedure を用いて推定したパラメータを代入した確率密度関数のグラフとヒストグラムを重ねて比較を行います。
%myhist(test, t, out);
data est;
if _n_ = 1 then set ESTDF;
do midpoint = -10 to 10 by 0.05;
dist = pdf("t", midpoint, estimate);
distn = pdf("normal", midpoint);
output;
end;
call symput("estdf", compress(round(estimate, 0.01)));
run;
data out; set out est;
proc sort data = out; by midpoint;
goptions reset = all;
goptions vsize = 12 in hsize = 19 in htitle = 3.5 htext = 3.5;
filename grafout "&path.test1.bmp";
goptions device = bmp gsfname = grafout gsfmode = replace;
goptions ftext = "Times New Roman";
proc gplot data = out;
plot (density dist distn) * midpoint /
noframe skipmiss overlay autovref cautovref = cxE9DECA
legend = legend1 haxis = axis1 vaxis = axis2;
axis1 label = ("t") order = (-10 to 10 by 2) minor = none;
axis2 label = (a = 90 "Density") order = (0 to 0.4 by 0.05)
minor = none;
symbol1 i = needle v = none w = 10 c = "cxE41A1C";
symbol2 i = joins v = none w = 5 c = "cx377EB8";
symbol3 i = joins v = none w = 5 c = "cx4DAF4A";
legend1 position = (top right inside) across = 1
offset = (-1, -1) label = none mode = share shape = line(10)
value = (" Histogram" " t(df = &estdf.)" " N(0, 1)");
run;
out というデータセットにヒストグラム用のデータが作成され、変数 dist にパラメータ推定値を代入した t 分布の密度を計算します、ついでに標準正規分布の密度も変数 distn に計算しています。このデータを GPLOT procedure を用いて可視化します、symbol statement の i = neelde オプションで棒グラフを描画できます。上のスクリプトを実行すると、以下の図が作成されました。
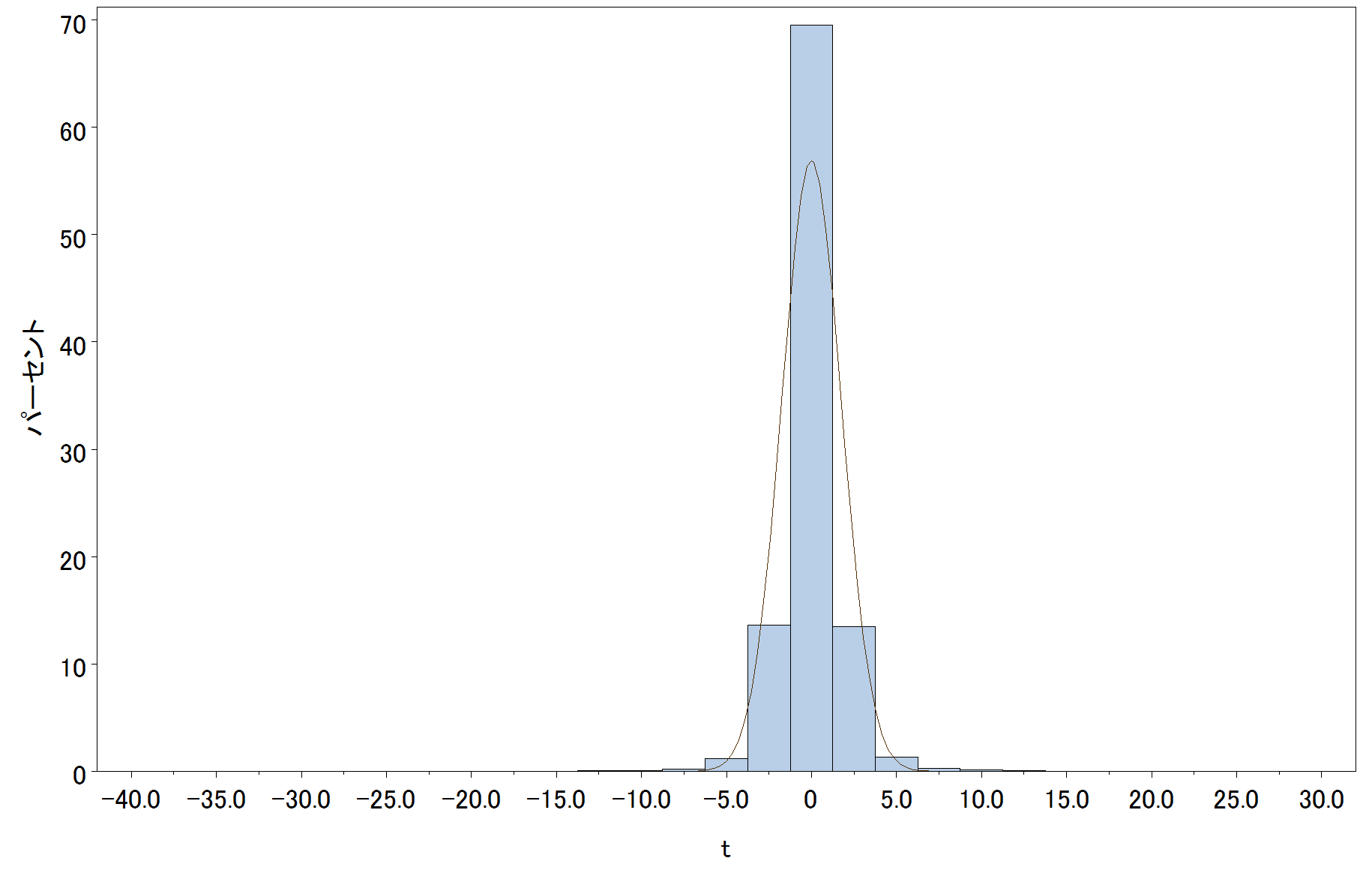
UNIVERIATE procedure の例
goptions reset = all;
goptions vsize = 12 in hsize = 19 in htitle = 3 htext = 3;
filename grafout "&path.test2.bmp";
goptions device = bmp gsfname = grafout gsfmode = replace;
proc univariate data = test;
var t;
histogram t / normal(mu = est sigma = est);
run;
SAS スクリプト
履歴
- 2011/12/22 公開